HEATS OF VAPORIZATION

The heat of vaporization of a liquid is a useful thermodynamic quantity because it allows the calculation of the vapor pressure of the liquid at any temperature.

Two practical applications of heats of vaporization are distillations and vapor pressure:

• Distillation is one of the most practical methods for separation and purification of chemical compounds. The heat of vaporization is the fundamental quantity that determines the experimental conditions at which an industrial or laboratory-scale distillation should be run.
• The concentration of a gas is given by its vapor pressure. Knowledge of the heat of vaporization permits the control of vapor pressure by setting the temperature of the liquid being vaporized.

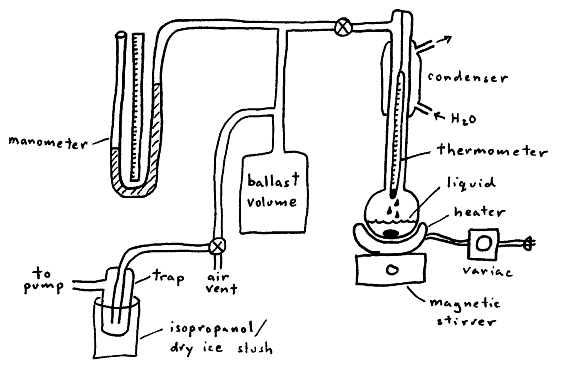
In this apparatus, the pump and air vent allow control the system pressure. The liquid is heated until it boils under the applied pressure of the system. Since a liquid boils when its vapor pressure equals the applied external pressure, the vapor pressure of the liquid at a given temperature is known by reading the manometer and thermometer. (The only unusual aspect of this experimental arrangement is that pressure is the independent variable, while temperature is the dependent variable.) The purpose of the condenser to reduce the amount of organic vapor entering the rest of the system, and the purpose of the ballast volume is to absorb small volume changes as the system is heated or cooled.

Two phases in equilibrium at constant pressure and temperature have the same Gibb’s free energy. Recalling that dG = Vdp - SdT yields

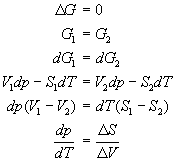
For a phase transition occurring at constant temperature and pressure, the definition of entropy dS = dq/T implies that D S_transition = D H_transition/T. Thus,

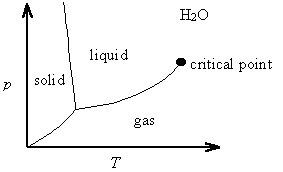
The Clapeyron equation is valid along any phase co-existence line. It explains, for example, that the solid-liquid phase co-existence line for water has a negative slope in a p vs. T phase diagram, since the change in volume in going from ice to water is negative (ice floats in water).

When the Clapeyron equation is applied to liquid-vapor phase co-existence, several simplifying assumptions can be made.

First, since the volume of a gas is much greater than the volume of a condensed phase,

Second, the gas is assumed to obey the ideal gas law

which allows the Clapyron equation to be simplified as follows

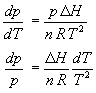
Third, DH is assumed to be independent of temperature and pressure, allowing indefinite integration over p and T

Choosing the constant of integration to equal ln p₀, where p₀ equals one pressure unit, e.g., 1 Torr if pressure is measured in Torr, allows the pressure units to cancel and yields

This equation is useful for determining DH from a plot of ln (p/p₀) vs. 1/T.

If definite integration from p₁ to p₂ and from T₁ to T₂ is performed, the result is

This equation is useful for determining the vapor pressure p₂ at temperature T₂ given DH and the vapor pressure at one temperature (p₁, T₁), e.g., the normal boiling point.

In this experiment, (vapor pressure, temperature) data pairs are measured over the pressure range from about 100 Torr to ambient pressure.

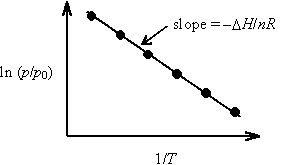
A plot of ln (p/p₀) vs. 1/T is constructed, and the slope is interpreted to be according to the indefinite form of the Clausius-Clapeyron equation. The quantity DH/n is interpreted as D_vapH, the molar enthalpy of vaporization.

A real Clausius-Clapeyron often shows some slight curvature. This curvature can be analyzed by considering the limitations of the three approximations made during the derivation of Clausius-Clapeyron equation from the rigorously correct Clapeyron equation.

The non-ideal behavior exhibited by a real gas is often represented by the compression factor Z defined by

For an ideal gas, Z equals unity. For saturated vapor, Z decreases with increasing temperature as the critical point is approached and the gas becomes more like a liquid.

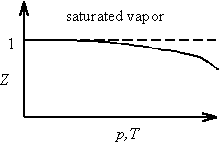
The effect of non-ideal gas behavior on the Clausius-Clapeyron equation can be seen by replacing V_ideal = nRT/p with V_real = ZnRT/p. Assuming Z to be independent of p and T for purposes of integration (which is actually a poor numerical approximation, especially near the critical point) yields

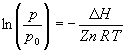
Thus, as temperature increases on a Clausius-Clapeyron plot, Z decreases and the slope (=-DH/ZnR) increases. This results in upward curvature of the plot.

5. B. Temperature dependence of DH

The enthalpy of vaporization can strongly depend on temperature. In fact, D_vapH approaches zero as the liquid-vapor co-existence line approaches the critical point, as there is no distinction between liquid and vapor at temperatures and pressures above the critical point!

As temperature increases on a Clausius-Clapeyron plot, DH decreases and the slope (=-DH/ZnR) decreases. This results in downward curvature of the plot.

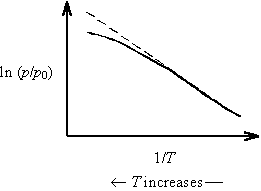
Notice that the non-ideality of real gas and the temperature dependence of DH have opposite effects. It turns out that these effects are each quite significant; however, they very nearly cancel each other out! Hence, Clausius-Clapeyron plots tend to be quite linear. See Waldenstrom et al., Journal of Chemical Education 59, 30 (1982) for a discussion of these effects.

The effect of V_liq can be incorporated into the Clausius-Clapeyron equation by writing

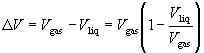
Assuming (1 - V_liq/V_gas) to be independent of temperature for purposes of integration (which is a reasonable approximation only over a small temperature range and far from the critical point) yields

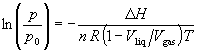
The slope must be multiplied by -(1 - V_liq/V_gas) R to obtain D_vapH. Since (1 - V_liq/V_gas) is slightly less than one, neglecting this factor slightly overestimates D_vapH, e.g., by less than 0.1%.

• Answer the question "Why do some foods come with high altitude cooking instructions?" Give your answer in thermodynamic and kinetic terms.
• Ask someone who is not a Hope College Chemist the same question "Why do some foods come with high altitude cooking instructions?" Then answer the following questions
  A) What is this person’s chemistry background?
  B) What was this person’s answer?
  C) Did this person answer the question correctly?
• As a Chemistry 345 student, you are responsible for making sure that your volunteer learns the correct answer to this question. Do you think he or she understood your explanation?